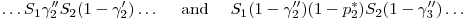www.phidot.org

Hi,

I am running a robust design analysis in Rmark with 12 primary periods and 53 secondary periods (secondary occasions varying from 2 to 7). Samples were collected every three months, except for two occasion, one with six month interval and another one with 12 month interval.

And this is how I am setting my time intervals on RMark:

Code: Select all

#Process data specifying primary and secondary capture occasions
time.intervals=c(0,0,0,0,0,3,0,0,3,0,3,0,0,0,3,0,0,0,0,0,3,0,0,0,0,3,0,0,0,0,12,0,0,0,3,0,0,0,0,0,3,0,0,3,0,0,6,0,0,0,0,0)
rd.process=process.data(rd.data,begin.time=1,model="Robust",time.intervals=time.intervals)


If I understood well from a post on this forum, the survival rates are corrected for this unequal time intervals, meaning that if I run a model with phi(year), I should get an estimate for each one of the four years of my study period, right?

For example,the following model:
S(~Year)Gamma''(~Year)Gamma'(~season)p(~-1 + session:time)c()f0(~session)

Parameter Estimate Standard Error Lower Upper
-------------------------- -------------- -------------- -------------- --------------
1:S g1 c1 c1 a0 t1 0.9799760 0.0067555 0.9614259 0.9897010
2:S g1 c1 c1 a12 t13 0.9925958 0.0027449 0.9847264 0.9964254
3:S g1 c1 c1 a30 t31 0.9972842 0.0022175 0.9866292 0.9994531
4:S g1 c1 c1 a36 t37 0.9990069 0.0012978 0.9872554 0.9999234

The survival times t1, t13, t31 and t37 match the beginning of each year,2006, 2007, 2008 and 2009?

Using the previous models, I get these gamma" estimates

5:Gamma'' g1 c1 c1 a0 0.4978534 0.0715431 0.3613535 0.6346741
6:Gamma'' g1 c1 c1 a12 0.3038718 0.0540613 0.2091856 0.4187238
7:Gamma'' g1 c1 c1 a30 0.1612076 0.0531546 0.0816796 0.2934269
8:Gamma'' g1 c1 c1 a36 0.0780162 0.0425256 0.0258719 0.2123465

Could I interpret this as that gamma" decrease from year 1 to 4 (0.49 to 0.07)?

Thanks
Sergi

You should check out section 15.9 in Bill Kendall's robust design chapter of the MARK book, which reads:

As noted in Chapter 10, any data type with state transitions suffers from the same problem when
the intervals between occasions are unequal (how MARK handles unequal intervals in general was
introduced earlier in Chapter 4).

<snip>

Given the deep connections between ‘multi-state’ models and ‘robust design’ models introduced in
this chapter, it is perhaps not surprising that the same general issue applies here. Consider the robust
design with 3 primary occasions, each with 2 secondary occasions. Assume that the data were not
collected for the 2nd primary sample, giving an encounter history of ‘11..11’. The missing primary
encounter history again can be explained by 2 possibilities:





For the robust design data type, coding the encounter history as only 2 primary occasions, ‘1111’,
with time interval of 2 will give the correct parametrization for S (i.e., S2), but as above, the γ' and γ" parameters cannot be corrected with this simple trick because the possibility of leaving the encounter area is not considered. So, for robust design data types (including the multi-state robust designs), only survival rates are corrected with the time interval, but none of the transition parameters are corrected. Again, user beware! Think carefully about what unequal time intervals may be doing to your interpretation of the parameter estimates.

If I give the unequal time intervals, I should get corrected for S, as the previous shown as S per year, right? And the S would increase per year.

To correct the gamma” and gamma’ could I incorporate covariates? As they have a specific values for each specific primary period.

A previous post on this forum early this year, it was mentioned that “When including dots "." for those missing primary periods in, for example, a Robust Design, you need to add a minimum of TWO DOTS PER PRIMARY PERIOD, that is, two secondary sessions per primary period,even though it was not sampled.

Would this be a solution for deal with unequal time intervals and get seasonal or yearly estimates?

Sergi,

One discussion on validity of "." for missing occasions:
viewtopic.php?f=1&t=2528&p=8018&hilit=coding+.+missing+occasion#p8018

I had unequal time intervals in my robust design models as well. I coded missing occasions as 0's in the encounter histories and then fixed all those missing occasions to 0 in the models. This is pretty easy in RMark using row indices and is outlined in section C.11 (Fixing real parameter values) in the Gentle MARK book. You can fix the same or different occasions for any of the parameters in robust design. I'm happy to send example code if you need it.

Sorry - I don't have any advice on how to interpret your gammas.

Joe

Joe,

I would appreciate an example with the missing occasions as 0's in the encounter histories and then fixed all those missing occasions to 0 in the model.
Does it has any influence when you do the parameters interpretation?

Sergi

After rereading your post, I'm not sure this properly addresses your questions, but here it is. Caveat: I'm relatively new to RMark myself, so hopefully someone else will comment if I'm leading you astray. Also, definitely read section C.11 from the Gentle Intro to MARK book if you haven't already. Jeff Laake does a much better job explaining this than I do (http://www.phidot.org/software/mark/docs/book/).

I had some unequal capture histories, e.g., some sites were surveyed more than others.
1001
101
110

Make all the histories equal by adding a 0 ("dummy" occasion) to the shorter histories :
1001
1010
1100

You can check the length of all the histories with something like:

Code: Select all

unique(nchar(MyData$ch))

Grab the row indices for the dummy occasions. I use R's subsetting syntax, but you could also check out the extract.indices function.

Code: Select all

p.indices <- as.numeric(row.names(MyData.ddl$p$session == "1" & MyData$p$time == "4" & MyData.ddl$p$site== "site1"))
 
# specify values (0) for p.indices
p.values <- rep(0, length(p.indices))

# You would repeat the same process for other parameters that need to be fixed,
#like c, and create separate objects, like c.indices and c.values, to be called in 
#the formula.

# Call the indices and values when you define the formula (could do this all within #the "mark" function)
p.dot <- list(formula = ~1, share = FALSE, fixed = list(index=p.indices, value=p.values))

# run model
mark(MyData.proc, MyData.ddl,
     model.parameters = list(GammaPrime=GammaPrime.dot, GammaDoublePrime=GammaDoublePrime.dot, S = s.formula, p = p.dot, c = c.formula))


One thing that hung me up was when you're running a model with share = TRUE (so you're not defining a formula for c) but still need to fix certain indices for p and c. This works:

Code: Select all

mark(pema.proc, pema.ddl,
     model.parameters = list(GammaPrime=GammaPrime.dot, GammaDoublePrime=GammaDoublePrime.dot, S = s.formula, p = p.dot,
c = list(fixed=list(index=c.indices, value=c.values))))

Hope that is somewhat clear and helpful.
Joe