I'm trying to replicate the results in this paper for the single release model. The estimators given on page 1487 are the same as given by Burham et al. (1987)and as derived by Cormack. Just to double check and to keep my derivation skills sharp, I also derived these estimators using maximum likelihood and the delta method for the variance. The reason I'm going through this is because I want to compare these "simple" algebraic estimators, the full model equivalent in MARK and marked, the implementation in SURPH, and a Bayesian implementation using JAGS. I'm not able to exactly replicate the result in the paper, but at this point that's a side issue. (I'm off by a very small amount to the results in Table 6 and 7, but the results I get using the algebraic estimators and the iterative MLE estimation in SURPH are in agreement, so I'm going to chalk it up to a typo.)
The bigger issue I have is that when I simulate data and take the mean of many estimates (50,000-100,000) the average of these estimates is always slightly larger than the true probability specified in the simulation. The magnitude of the differences seems to dependent on all the usual actors, i.e. sample size, and specific probabilities. But it can be as large as a half percent in some scenarios I've tried, and in the world of Pacific salmon survival studies a half percent can add up to millions of dollars in mitigation money. I just wanted to see if this was known feature of these estimators and that I just somehow missed the memo, or if this has been explored otherwise. My intuition is that the source of the bias is due to the inclusion of binomial random variables in the denominator of the estimator. E[1/X] doesn't necessarily equal 1/E[X], but it may be greater than (Jensen's inequality) and so I think that is the source of the inflation. I'm still working on the implementation to compare to marked and MARK through RMark, so I don't have a comparison with those estimators quite yet, but will update if there is interest.
Happy to share R code if there is an interest as well.
Cormac Jolly Seber estimators biased?
7 posts
• Page 1 of 1
Re: Cormac Jolly Seber estimators biased?
daltonhance wrote:I'm trying to replicate the results in this paper for the single release model. The estimators given on page 1487 are the same as given by Burham et al. (1987)and as derived by Cormack. Just to double check and to keep my derivation skills sharp, I also derived these estimators using maximum likelihood and the delta method for the variance. The reason I'm going through this is because I want to compare these "simple" algebraic estimators, the full model equivalent in MARK and marked, the implementation in SURPH, and a Bayesian implementation using JAGS. I'm not able to exactly replicate the result in the paper, but at this point that's a side issue. (I'm off by a very small amount to the results in Table 6 and 7, but the results I get using the algebraic estimators and the iterative MLE estimation in SURPH are in agreement, so I'm going to chalk it up to a typo.)
The bigger issue I have is that when I simulate data and take the mean of many estimates (50,000-100,000) the average of these estimates is always slightly larger than the true probability specified in the simulation. The magnitude of the differences seems to dependent on all the usual actors, i.e. sample size, and specific probabilities. But it can be as large as a half percent in some scenarios I've tried, and in the world of Pacific salmon survival studies a half percent can add up to millions of dollars in mitigation money. I just wanted to see if this was known feature of these estimators and that I just somehow missed the memo, or if this has been explored otherwise. My intuition is that the source of the bias is due to the inclusion of binomial random variables in the denominator of the estimator. E[1/X] doesn't necessarily equal 1/E[X], but it may be greater than (Jensen's inequality) and so I think that is the source of the inflation. I'm still working on the implementation to compare to marked and MARK through RMark, so I don't have a comparison with those estimators quite yet, but will update if there is interest.
Happy to share R code if there is an interest as well.
Decisions made on the basis of a point estimate, and not the estimate conditional on variance? No wonder we don't know how many fish there are.
I only have a moment, but my intuition tells me that: (i) any 'bias' (not the best word) is a function of time since release -- simple reason, marked sample gets smaller over time in a single release study, (ii) and is a function of the underlying parameter value. If the parameter (for, say, phi) is 0.5, then I suspect that the 'bias' is essentially 0 to within sampling error. If the true parameter is something close to the boundary( say, 0.85), then the problem might be that the mean of the samples is a not the best moment to use. Just put on your Bayesian hat -- think of a posterior (which is in effect what you're generating) -- mean, median, or mode? Smart folks say that focus on the point estimate is missing the point (pun intended) -- the credible interval is the important point. For parameters bounded on the interval [0,1], what is the expected distribution of bootstrapped samples given a true underlying parameter on that interval?
I did a completely exhaustive 10 minute simulation (ok, not exhaustive), and my basic results support both (i) and (ii)., with (i) being largely driven by underlying encounter probability. If I make it ~1.0, then I get the true estimate for phi out to at least 5 decimal places, for all intervals. As P -> 0, things get worse and worse over time, but not in any systematic way, if phi ~0.5. For example, true model phi(t)p(.). Release 1000 fishies over 6 occasions. True survival 0.5, encounter probability 0.2 (cue fish guys rolling eyes -- we'll pretend we're working with a cooperative fish that is easy to catch). 10,000 simulations. No error to within reason (say, average of 0.501 relative to 0.500 as true value) over first few encounters, slightly more, or less than that over time. More *or* less, meaning sometime the estimate is <0.5 (by some tiny amount -- well within Monte Carlo error).
If I tried the same thing with true underlying phi=0.9, but low p (say, 0.1), then mean>mode>median, with the disparity somewhat increasing the further away from the release occasion you get, since the distribution isn't *perfectly* normal (increasing left left skew). Problem might simply be analogous to taking the mean of the distribution of abundance from a stochastic time series based on a simple first-order Markov projection process. The distribution there is log-normal, so the mean would massively over-estimate the most likely realization. When I plot the distribution of real estimates, there is increasing left skew for latent parms near the [1] boundary, with increasing time since release.
Again, all of this is based on some pretty cursory simulations (to say the least), but in the end, all seems to match my intuition, and...in the end, the difference is within any reasonable Monte Carlo error, so...no, you didn't miss the memo.
- cooch
- Posts: 1665
- Joined: Thu May 15, 2003 4:11 pm
- Location: Cornell University
Re: Cormac Jolly Seber estimators biased?
Decisions made on the basis of a point estimate, and not the estimate conditional on variance? No wonder we don't know how many fish there are.
I'll refrain from making too much commentary here, since I'm just a little Statistical fish in Columbia River basin who wants to continue to draw a paycheck. But yes, there have been some decisions made out here on the basis of point estimates. Although there is also an emphasis on achieving estimated standard errors less than a specified amount. One interesting thing is that many of these decisions are based on agreements which require demonstrating survival standards that are very near the boundary (e.g. 93% passage survival for downstream migrating juvenile salmon.) It's especially interesting when you see published survival estimates greater than 1. But it is the way things are done out here. I have no comment on these practices. I'm simply trying to understand the mechanics of the estimators.
One more aside:
. Actually in the Columbia river with migratory (often hatchery-raised) smolts, you're not that far off. Detection efficiency estimates at McNary dam are typically around 0.15 - 0.20, and survival from the "Upper" Columbia River (Upper here meaning the river and tributaries below Grand Coullee Dam) can be right around 0.5. Of course these are estimates, based on the CJS estimators, but release groups sizes around 10,000 fish not being unreasonable. And if you're talking about a survival study using acoustic tags, you can get estimates of survival and detection both well above .90.True survival 0.5, encounter probability 0.2 (cue fish guys rolling eyes -- we'll pretend we're working with a cooperative fish that is easy to catch)
I dig your argument on the mean, median, mode. In my heart, I am a Bayesian. which is really the whole point of this exercise, seeing if, how and when a Bayesian model may be a better choice than the currently accepted standard practice. BUT, for the sake of this exercise I'm putting on my frequentist hat and simply looking at the long run properties of these estimators. Really I'm most interested in confidence interval coverage, but coverage is going to be affected by the mean square error of the estimators used. As part of that, I'm calculating bias (
![E[\hat{\theta}] - \theta E[\hat{\theta}] - \theta](/forum/latexrender/pictures/ab49becc2f7ce76e14dff96e72d6f8c1.gif) ) of the point estimator, which means I'm using the mean. I'm also interested in the estimator of the variance of the estimator, which is based on a delta method approximation, and how that compares to the actual simulated variance of estimator. (Spoiler alert: based on my cursory simulations, the delta method approximation tends to under estimate the actual standard error.)
) of the point estimator, which means I'm using the mean. I'm also interested in the estimator of the variance of the estimator, which is based on a delta method approximation, and how that compares to the actual simulated variance of estimator. (Spoiler alert: based on my cursory simulations, the delta method approximation tends to under estimate the actual standard error.) Obviously, these are all sensitive to sample size as well as the underlying parameter value. You said you used 6000 fish over 6 releases, I was seeing a upward bias on the order of a tenth to half percentage point or so of bias using only 500 fish in one release. (3 detection occasions, true phi.1 = .5, mean of estimated phi=.5017, true phi.2 =.8, mean of estimated phi=.8057, p.2=.475, p.3 = .525).
- daltonhance
- Posts: 4
- Joined: Thu Oct 31, 2013 7:20 pm
Re: Cormac Jolly Seber estimators biased?
daltonhance wrote:Obviously, these are all sensitive to sample size as well as the underlying parameter value. You said you used 6000 fish over 6 releases, I was seeing a upward bias on the order of a tenth to half percentage point or so of bias using only 500 fish in one release. (3 detection occasions, true phi.1 = .5, mean of estimated phi=.5017, true phi.2 =.8, mean of estimated phi=.8057, p.2=.475, p.3 = .525).
No, I used a single release of 1,000 fishies on the first occasion of a 6 occasion study, which is what I thought you were describing in your original note (i.e., analogous to a batch release, follow over time). In that case, sample of marked fish declines over time, which means that there is a greater likelihood of Monte Carlo error in later samples. Systematic bias relative to true parameter is probably an artifact of temporal change in sample size, exacerbated by low p, and phi near a boundary. The histogram of bootstrapped estimates of phi when you're up near a boundary is anything but 'normal' (or even symmetrical), meaning I'd not be sanguine about using the the mean as the most appropriate moment to describe the distribution. But, I've had a long-standing discomfort with any approach that defaults to the mean as the best descriptor of the 'posterior', since it makes rather strong assumptions about the symmetry (at least) of the distribution around the moments. I very frequently run up against strong asymmetrical posteriors, and have struggled with the operational need (in some cases) to come up with a point estimate. Less critical for (say) use in a stochastic projection, where I can use the pattern of variation directly, but for people (or uses) that requirte 'th number', no always obvious what number to use.
In your case, might be worth trying the experiment of setting true survival to 0.5. You've clearly done a lot more thinking and coding, so it would probably be straightforward to evaluate whether my prediction and somewhat supported observation that the 'result' your originally described is an artifact of asymmetry in the bootstrap distribution, which in itself is an artifact of where the parameter falls relative to the [0,1] boundaries.
Neat question.
- cooch
- Posts: 1665
- Joined: Thu May 15, 2003 4:11 pm
- Location: Cornell University
Re: Cormac Jolly Seber estimators biased?
Hey Cooch, thanks for taking the time to dig into this a little bit. I had started to reply to you yesterday, but took so long to write it that phidot asked me to log back in and I lost the post. All the better, because it gave me the impetus to play around a bit more. One quick bit of apology:
I'm with you now and would've been with you before if I had only taken the time to properly read what you wrote.
Mimicking Skalski et al. I started out by playing around with fewer occasion, only 3 detection events and single release for a 4 column detection history matrix. Based on your observation that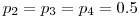 and
and 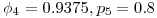 such that
such that 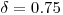 . The three simulation scenarios were 1.
. The three simulation scenarios were 1. 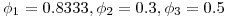 and 2.
and 2. 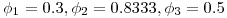 and 3.
and 3. 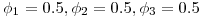 . Thus we would expect 250 fish to remain for the third detection event in all three scenarios. For each simulation I randomly generated 10,000 datasets and estimated survival and detection parameters using the single-release CJS estimators outlined in Skalski et al. 1998. What follows is brief tour of what I learned about CJS survival estimators and an interesting (to me, at least) exploration of the properties of the confidence intervals for the estimates.
. Thus we would expect 250 fish to remain for the third detection event in all three scenarios. For each simulation I randomly generated 10,000 datasets and estimated survival and detection parameters using the single-release CJS estimators outlined in Skalski et al. 1998. What follows is brief tour of what I learned about CJS survival estimators and an interesting (to me, at least) exploration of the properties of the confidence intervals for the estimates.
So first off, how did the estimators do? It looks like when the true parameter values was greater (not further away from 0.5), the "bias" was slightly worse, but the temporal change in sample size was more of a dominant force:
Simulation 1:
The mean of the estimates differs from true parameter values of around 0.0043, 0.0026, and 0.0153.
Simulation 2:
The mean of the estimates differs from true parameter values of around 0.0009, 0.0066, and 0.0135.
Simulation 3:
The mean of the estimates differs from true parameter values of around 0.0023, 0.0035, and 0.0168.

Ok, so that's the point estimates. What about confidence intervals? Standard errors were calculated using the equations provided in Skalski et al. and I made use of the normality assumption (despite just pointing out that it might not hold) to calculate 95% confidence intervals as the estimate plus or minus 1.96 times the standard error. Then I checked to see how many times in the simulation the true parameter was actually in the CIs.
Simulation 1:
Simulation 2:
Simulation 3:
Hey! Not too shabby. But wait, how does that square with the bias I'm seeing where some estimates tend to be quite large? Maybe these CIs aren't symmetrical?
Simulation 1:
Simulation 2:
Simulation 3:
Well that's not what I expected. The CIs aren't symmetrical, but if the true estimate lies outside the interval, generally speaking, it's because it's actually greater than the upper confidence limit! Actually, in the scenarios where we tend to get really bad overestimates ([tex]\phi_3[\tex] after winnowing of the original sample size) the estimate is almost never below the lower confidence limit. That looks like this:

What's going on here? It turns out that the estimated standard error depends on the estimate itself and that both are affected by sample size:

So what did I learn here? Well, probably nothing too exciting. It turns out that yes, the CJS estimators can be biased, but that this is largely an effect of sample size. Somewhere my old Stat's professor is going "no duh", because the MLEs of CJS are like all MLEs asymptotically consistent. And I learned that I should maybe distrust estimates of survival further from the release due to the winnowing of sample size. I also learned that 1000 fish might not cut it.
RCode below for those interested:
No, I used a single release of 1,000 fishies on the first occasion of a 6 occasion study, which is what I thought you were describing in your original note (i.e., analogous to a batch release, follow over time).
I'm with you now and would've been with you before if I had only taken the time to properly read what you wrote.
In my heart, I'm with you. But for this exercise I'm firmly seated in my frequentist's britches. That means that the true parameter is fixed, data are random, and while we care about how an estimator performs over the long run, in practice we only usually have one estimate and it might be particularly good or particularly bad. For this exercise I just want to know how the estimator performs, and so was going with the frequentist definition of bias. But your comments got me thinking about exploring the long run properties of the estimator by looking at more than just the mean. Here's what I found out:Just put on your Bayesian hat -- think of a posterior (which is in effect what you're generating) -- mean, median, or mode? Smart folks say that focus on the point estimate is missing the point (pun intended) -- the credible interval is the important point.
Mimicking Skalski et al. I started out by playing around with fewer occasion, only 3 detection events and single release for a 4 column detection history matrix. Based on your observation that
I bumped that up to 4 detection events, for a 5 column detection history matrix. I performed three simulations, keeping the following fixed: initial sample size of n=1500,Systematic bias relative to true parameter is probably an artifact of temporal change in sample size, exacerbated by low p, and phi near a boundary.
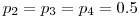 and
and 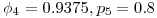 such that
such that 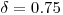 . The three simulation scenarios were 1.
. The three simulation scenarios were 1. 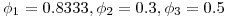 and 2.
and 2. 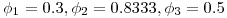 and 3.
and 3. 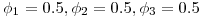 . Thus we would expect 250 fish to remain for the third detection event in all three scenarios. For each simulation I randomly generated 10,000 datasets and estimated survival and detection parameters using the single-release CJS estimators outlined in Skalski et al. 1998. What follows is brief tour of what I learned about CJS survival estimators and an interesting (to me, at least) exploration of the properties of the confidence intervals for the estimates.
. Thus we would expect 250 fish to remain for the third detection event in all three scenarios. For each simulation I randomly generated 10,000 datasets and estimated survival and detection parameters using the single-release CJS estimators outlined in Skalski et al. 1998. What follows is brief tour of what I learned about CJS survival estimators and an interesting (to me, at least) exploration of the properties of the confidence intervals for the estimates.So first off, how did the estimators do? It looks like when the true parameter values was greater (not further away from 0.5), the "bias" was slightly worse, but the temporal change in sample size was more of a dominant force:
Simulation 1:
- Code: Select all
> mean(phi.ests[,1])
[1] 0.8376835
> mean(phi.ests[,2])
[1] 0.3026313
> mean(phi.ests[,3])
[1] 0.5153572
The mean of the estimates differs from true parameter values of around 0.0043, 0.0026, and 0.0153.
Simulation 2:
- Code: Select all
> mean(phi.ests[,1])
[1] 0.3009724
> mean(phi.ests[,2])
[1] 0.8399773
> mean(phi.ests[,3])
[1] 0.5135659
The mean of the estimates differs from true parameter values of around 0.0009, 0.0066, and 0.0135.
Simulation 3:
- Code: Select all
> mean(phi.ests[,1])
[1] 0.5023404
> mean(phi.ests[,2])
[1] 0.5034649
> mean(phi.ests[,3])
[1] 0.5167618
The mean of the estimates differs from true parameter values of around 0.0023, 0.0035, and 0.0168.
But recall here in the mythical land of Frequencia maximum likelihood estimators are normal in the province of Asymtopia. I don't think we've quite reached the border with of that province, but one surprising result is that even though the mean of the estimates is generally higher than the true value, the median is spot on. So at least we can say that about half the time we'll be underestimating and half the time overestimating, it's just that when you overestimate, you can sometimes badly overestimate. Here is a histogram, arbitraily from the third simulation where all phi's are equal. Blue dashed line is the mean, the green dotted line is median, red line is true parameter value. So yes the mean is not the best descriptor of the distribution of the estimates, but as I said up above, in practice, we don't get 10,000 estimates. We usually only get one and try to make policy off it:The histogram of bootstrapped estimates of phi when you're up near a boundary is anything but 'normal' (or even symmetrical), meaning I'd not be sanguine about using the the mean as the most appropriate moment to describe the distribution.

Ok, so that's the point estimates. What about confidence intervals? Standard errors were calculated using the equations provided in Skalski et al. and I made use of the normality assumption (despite just pointing out that it might not hold) to calculate 95% confidence intervals as the estimate plus or minus 1.96 times the standard error. Then I checked to see how many times in the simulation the true parameter was actually in the CIs.
Simulation 1:
- Code: Select all
> sum(phi.1<(phi.ests[,1]+1.96*SE.S.ests[,1]) & phi.1>(phi.ests[,1]-1.96*SE.S.ests[,1]))/m
[1] 0.9499
> sum(phi.2<(phi.ests[,2]+1.96*SE.S.ests[,2]) & phi.2>(phi.ests[,2]-1.96*SE.S.ests[,2]))/m
[1] 0.9527
> sum(phi.3<(phi.ests[,3]+1.96*SE.S.ests[,3]) & phi.3>(phi.ests[,3]-1.96*SE.S.ests[,3]))/m
[1] 0.9484
Simulation 2:
- Code: Select all
> sum(phi.1<(phi.ests[,1]+1.96*SE.S.ests[,1]) & phi.1>(phi.ests[,1]-1.96*SE.S.ests[,1]))/m
[1] 0.9519
> sum(phi.2<(phi.ests[,2]+1.96*SE.S.ests[,2]) & phi.2>(phi.ests[,2]-1.96*SE.S.ests[,2]))/m
[1] 0.949
> sum(phi.3<(phi.ests[,3]+1.96*SE.S.ests[,3]) & phi.3>(phi.ests[,3]-1.96*SE.S.ests[,3]))/m
[1] 0.9482
Simulation 3:
- Code: Select all
> sum(phi.1<(phi.ests[,1]+1.96*SE.S.ests[,1]) & phi.1>(phi.ests[,1]-1.96*SE.S.ests[,1]))/m
[1] 0.9467
> sum(phi.2<(phi.ests[,2]+1.96*SE.S.ests[,2]) & phi.2>(phi.ests[,2]-1.96*SE.S.ests[,2]))/m
[1] 0.9484
> sum(phi.3<(phi.ests[,3]+1.96*SE.S.ests[,3]) & phi.3>(phi.ests[,3]-1.96*SE.S.ests[,3]))/m
[1] 0.9477
Hey! Not too shabby. But wait, how does that square with the bias I'm seeing where some estimates tend to be quite large? Maybe these CIs aren't symmetrical?
Simulation 1:
- Code: Select all
> 1-sum(phi.1<(phi.ests[,1]+1.96*SE.S.ests[,1]))/m
[1] 0.0393
> 1-sum(phi.1>(phi.ests[,1]-1.96*SE.S.ests[,1]))/m
[1] 0.0108
> 1-sum(phi.2<(phi.ests[,2]+1.96*SE.S.ests[,2]))/m
[1] 0.0374
> 1-sum(phi.2>(phi.ests[,2]-1.96*SE.S.ests[,2]))/m
[1] 0.0099
> 1-sum(phi.3<(phi.ests[,3]+1.96*SE.S.ests[,3]))/m
[1] 0.0504
> 1-sum(phi.3>(phi.ests[,3]-1.96*SE.S.ests[,3]))/m
[1] 0.0012
Simulation 2:
- Code: Select all
> 1-sum(phi.1<(phi.ests[,1]+1.96*SE.S.ests[,1]))/m
[1] 0.0321
> 1-sum(phi.1>(phi.ests[,1]-1.96*SE.S.ests[,1]))/m
[1] 0.016
> 1-sum(phi.2<(phi.ests[,2]+1.96*SE.S.ests[,2]))/m
[1] 0.0422
> 1-sum(phi.2>(phi.ests[,2]-1.96*SE.S.ests[,2]))/m
[1] 0.0088
> 1-sum(phi.3<(phi.ests[,3]+1.96*SE.S.ests[,3]))/m
[1] 0.0497
> 1-sum(phi.3>(phi.ests[,3]-1.96*SE.S.ests[,3]))/m
[1] 0.0021
Simulation 3:
- Code: Select all
> 1-sum(phi.1<(phi.ests[,1]+1.96*SE.S.ests[,1]))/m
[1] 0.0402
> 1-sum(phi.1>(phi.ests[,1]-1.96*SE.S.ests[,1]))/m
[1] 0.0131
> 1-sum(phi.2<(phi.ests[,2]+1.96*SE.S.ests[,2]))/m
[1] 0.0418
> 1-sum(phi.2>(phi.ests[,2]-1.96*SE.S.ests[,2]))/m
[1] 0.0098
> 1-sum(phi.3<(phi.ests[,3]+1.96*SE.S.ests[,3]))/m
[1] 0.0501
> 1-sum(phi.3>(phi.ests[,3]-1.96*SE.S.ests[,3]))/m
[1] 0.0022
Well that's not what I expected. The CIs aren't symmetrical, but if the true estimate lies outside the interval, generally speaking, it's because it's actually greater than the upper confidence limit! Actually, in the scenarios where we tend to get really bad overestimates ([tex]\phi_3[\tex] after winnowing of the original sample size) the estimate is almost never below the lower confidence limit. That looks like this:

What's going on here? It turns out that the estimated standard error depends on the estimate itself and that both are affected by sample size:

So what did I learn here? Well, probably nothing too exciting. It turns out that yes, the CJS estimators can be biased, but that this is largely an effect of sample size. Somewhere my old Stat's professor is going "no duh", because the MLEs of CJS are like all MLEs asymptotically consistent. And I learned that I should maybe distrust estimates of survival further from the release due to the winnowing of sample size. I also learned that 1000 fish might not cut it.
RCode below for those interested:
- Code: Select all
Single.Rls<-function(x){
#x is a capture history matrix
k<-ncol(x) #number of events
m<-matrix(rep(NA, k^2), ncol=k) #
R<-rep(NA, k-1)
for(i in 1:(k-1)){
for(j in (i+1):k){
m[i,j]<-sum(x[,i]==1 & rowSums(x[,i:j])==2 & x[,j]==1)+sum(x[,i]==1 & rowSums(x[,i:j])==3 & x[,j]==2)
}
R[i]<-sum(x[,i]==1)
}
#m<-m[1:k-1,2:k]
r<-rowSums(m, na.rm=T)[1:(k-1)]
M<-colSums(m, na.rm=T)[2:(k-1)]
z<-rep(NA,length(M))
for(j in 2:(k-1)){z[j-1]<-sum(m[1:(j-1),(j+1):k], na.rm=T)}
Tot<-M+z
S<-r[1:(k-2)]/R[1:(k-2)]*(M/Tot+(z*R[2:(k-1)])/(Tot*r[2:(k-1)]))
p<-M/(M+z*R[2:(k-1)]/r[2:(k-1)])
Var.S<-S^2*(1/r[1:(k-2)]-1/R[1:(k-2)]+(1-p)^2*(1/r[2:(k-1)]-1/R[2:(k-1)]))+
S^2*(1-p)^2*(1-r[2:(k-1)]/R[2:(k-1)])^2*(M/(z*Tot))
return(list(S.est=S, p.est=p, Est.VarS=Var.S, Est.SE.S=sqrt(Var.S)))
}
phi.1<-.5
phi.2<-.5
phi.3<-.5
phi.4<-.9375
p.2<-.5
p.3<-.5
p.4<-.5
p.5<-.8
n<-1000
m<-10000
phi.ests<-cbind(rep(NA,m), rep(NA,m), rep(NA,m))
p.ests<-cbind(rep(NA,m), rep(NA,m), rep(NA,m))
SE.S.ests<-cbind(rep(NA,m), rep(NA,m), rep(NA,m))
for(j in 1:m){
x<-matrix(rep(NA,5*n), ncol=5)
x[,1]<-rep(1,n)
#y is latent matrix of survival, absent detection problems
y<-x
y[,2]<-rbinom(n,1,phi.1)
x[,2]<-rbinom(n,1,p.2*y[,2])
y[,3]<-rbinom(n,1,phi.2*y[,2])
x[,3]<-rbinom(n,1,p.3*y[,3])
y[,4]<-rbinom(n,1,phi.3*y[,3])
x[,4]<-rbinom(n,1,p.4*y[,4])
y[,5]<-rbinom(n,1,phi.3*y[,4])
x[,5]<-rbinom(n,1,p.4*y[,5])
phi.ests[j,]<-Single.Rls(x)$S.est
p.ests[j,]<-Single.Rls(x)$p.est
SE.S.ests[j,]<-Single.Rls(x)$Est.SE.S
}
mean(phi.ests[,1])
mean(phi.ests[,2])
mean(phi.ests[,3])
mean(p.ests[,1])
mean(p.ests[,2])
mean(p.ests[,3])
sum(phi.1<(phi.ests[,1]+1.96*SE.S.ests[,1]) & phi.1>(phi.ests[,1]-1.96*SE.S.ests[,1]))/m
sum(phi.2<(phi.ests[,2]+1.96*SE.S.ests[,2]) & phi.2>(phi.ests[,2]-1.96*SE.S.ests[,2]))/m
sum(phi.3<(phi.ests[,3]+1.96*SE.S.ests[,3]) & phi.3>(phi.ests[,3]-1.96*SE.S.ests[,3]))/m
1-sum(phi.1<(phi.ests[,1]+1.96*SE.S.ests[,1]))/m
1-sum(phi.1>(phi.ests[,1]-1.96*SE.S.ests[,1]))/m
1-sum(phi.2<(phi.ests[,2]+1.96*SE.S.ests[,2]))/m
1-sum(phi.2>(phi.ests[,2]-1.96*SE.S.ests[,2]))/m
1-sum(phi.3<(phi.ests[,3]+1.96*SE.S.ests[,3]))/m
1-sum(phi.3>(phi.ests[,3]-1.96*SE.S.ests[,3]))/m
Estimates<-data.frame(Param=c(rep("Phi.1",m),rep("Phi.2",m), rep("Phi.3",m)),True=c(rep(phi.1,m),rep(phi.2,m), rep(phi.3,m)),
Est=c(phi.ests[,1], phi.ests[,2], phi.ests[,3]), SE=c(SE.S.ests[,1], SE.S.ests[,2], SE.S.ests[,3]))
par(mfrow=c(3,1))
hist(phi.ests[,1], breaks=75, main="10,000 estimates of phi.1=.5, n=1000")
abline(v=phi.1, col="red", lwd=2)
abline(v=mean(phi.ests[,1]), col="steelblue", lwd=2, lty=2)
abline(v=median(phi.ests[,1]), col="green", lwd=2, lty=3)
hist(phi.ests[,2], breaks=75, main="10,000 estimates of phi.2=.5, n=1000")
abline(v=phi.2, col="red", lwd=2)
abline(v=mean(phi.ests[,2]), col="steelblue", lwd=2, lty=2)
abline(v=median(phi.ests[,2]), col="green", lwd=2, lty=3)
hist(phi.ests[,3], breaks=75, main="10,000 estimates of phi.2=.5, n=1000")
abline(v=phi.3, col="red", lwd=2)
abline(v=mean(phi.ests[,3]), col="steelblue", lwd=2, lty=2)
abline(v=median(phi.ests[,3]), col="green", lwd=2, lty=3)
library(ggplot2)
ggplot(filter(Estimates.scen3, Param=="Phi.1") %>% arrange(Est), aes(y=Est, x=c(1:m)))+
geom_point()+geom_errorbar(aes(ymin=Est-1.96*SE, ymax=Est+1.96*SE), alpha=.1)+
geom_abline(intercept=phi.1, slope=0, colour="red", size=1.25)
ggplot(filter(Estimates.scen3, Param=="Phi.2") %>% arrange(Est), aes(y=Est, x=c(1:m)))+
geom_point()+geom_errorbar(aes(ymin=Est-1.96*SE, ymax=Est+1.96*SE), alpha=.1)+
geom_abline(intercept=phi.2, slope=0, colour="red", size=1.25)
ggplot(filter(Estimates.scen3, Param=="Phi.3") %>% arrange(Est), aes(y=Est, x=c(1:m)))+
geom_point()+geom_errorbar(aes(ymin=Est-1.96*SE, ymax=Est+1.96*SE), alpha=.1)+
geom_abline(intercept=phi.3, slope=0, colour="red", size=1.25)
ggplot(Estimates.scen3, aes(x=Est, y=SE))+geom_point()+facet_wrap(~Param)+
geom_vline(aes(xintercept=c(True)))
- daltonhance
- Posts: 4
- Joined: Thu Oct 31, 2013 7:20 pm
Re: Cormac Jolly Seber estimators biased?
daltonhance wrote:Hey Cooch, thanks for taking the time to dig into this a little bit. I had started to reply to you yesterday, but took so long to write it that phidot asked me to log back in and I lost the post.
Yes, it will do that. I created the forum with that 'feature' built in (not to keep the long-winded at bay, but to prevent long logins while an 'editor' window is open -- hackers love to camp out in such environments and do 'nasty things'. Putting a time-out function in the code reduces that risk). My general suggestion to folks is, if you're going to have a lengthy reply that will take some time to compose, do it external to the forum, then simply cut and paste.
Will read the rest of your note more carefully tomorrow. But, did see the bit about CI's. In general, the classical SE-based CI isn't preferred. MARK generates those as a computational convenience. At the end of the day, you should be thinking about CI's based on the profile likelihood. MARK doesn't do that by default, and I don't think Skalski talks about them at all (but I could be wrong).
- cooch
- Posts: 1665
- Joined: Thu May 15, 2003 4:11 pm
- Location: Cornell University
Re: Cormac Jolly Seber estimators biased?
Skalski does talk about profile likelihood CIs in the 1998 paper and they are implemented in SURPH. As you point out though, computational convenience makes the Wald CIs more attractive (especially considering 10,000 simulations). At this point, I'm not sure if it would be more time-consuming to try to write some R fuctions to interact with SURPH or to try to replicate maximizing the likelihood and profile likelihood in R. marked already use optimx to maximize likelihood, and this morning I wrote some code to compare marked estimates and CIs to the simple single release estimates and Wald CIs to the marked estimates and CI, but I'm not sure that Jeff and company have implemented profile likelihood CIs...
It'd be neat to compare these naive single-release estimates and Wald CIs which are maximized on the natural parameter space and so can be greater than 1, to the marked estimates and Wald CIs, to profile likelihood CIs,to the equivalent Bayesian credible intervals. I'm going there eventually, but just sort of reporting on the fly here. Thanks for humoring me on this.
It'd be neat to compare these naive single-release estimates and Wald CIs which are maximized on the natural parameter space and so can be greater than 1, to the marked estimates and Wald CIs, to profile likelihood CIs,to the equivalent Bayesian credible intervals. I'm going there eventually, but just sort of reporting on the fly here. Thanks for humoring me on this.
- daltonhance
- Posts: 4
- Joined: Thu Oct 31, 2013 7:20 pm
7 posts
• Page 1 of 1
Return to analysis & design questions
Who is online
Users browsing this forum: No registered users and 1 guest