Plotting environmental covariate relationships

[jlaake]

An often asked question on this sub-forum has been "How do I plot estimates for a range of environmental covariates". Environmental covariates are group or time-dependent and are the same for all animals so they are NOT individual covariates. Environmental (design) covariates are plugged directly into the design matrix so there isn't a direct way to modify those values. Individual covariates are stored as a name in the design matrix, so prediction for a range of values is easily done by substituting values into the name. One solution is to create time-varying individual covariates from environmental covariates where each individual covariate has the same value for each animal and there is an individual covariate for each time. With an individual covariate you can use the function covariate.predictions available for computing and plotting estimates for a range of covariate values.

Here is an example with the dipper data using made up rain levels instead of flooding. I create a model in which rain is a design covariate and then I create 6 individual covariates specifically named r1,r2,...r6 to match the time values of 1 to 6. r1 differs from say r2 but all the values of r1 are the same. Evan has used the same example in the sidebar at the end of section 11.5 to show how the same thing can be done with the MARK interface. You get the same estimates if you treat the covariates as design or individual covariates but using as an individual covariates let's you get predictions easily.

Code: Select all

library(RMark)
data(dipper)
# add a time varying covariate for Phi named to match beginning time of each time interval (default begin.time=1 and time.intervals=1)(r1,r2,..r6)
dipper$r1=rep(1,294)
dipper$r2=rep(10,294)
dipper$r3=rep(8,294)
dipper$r4=rep(15,294)
dipper$r5=rep(3,294)
dipper$r6=rep(6,294)
# process data
dp=process.data(dipper)
# create default design data
ddl=make.design.data(dp)
# add rain environmental covariate to design data for Phi; this matches r1 to r6.
ddl$Phi$rain=1
ddl$Phi$rain[ddl$Phi$time==2]=10
ddl$Phi$rain[ddl$Phi$time==3]=8
ddl$Phi$rain[ddl$Phi$time==4]=15
ddl$Phi$rain[ddl$Phi$time==5]=3
ddl$Phi$rain[ddl$Phi$time==6]=6
# fit model using design covariate
modcov=mark(dp,ddl,model.parameters=list(Phi=list(formula=~rain)))
# fit model using individual covariate
modicov=mark(dp,ddl,model.parameters=list(Phi=list(formula=~r)))
# get and plot predictions using individual covariates
predictions=covariate.predictions(modicov,data=data.frame(r1=0:20),indices=1)$estimates
with(predictions,
{
plot(0:20,estimate,xlab="Rain",ylab="Survival",ylim=c(0,1))
lines(0:20,lcl,lty=2)
lines(0:20,ucl,lty=2)
})


[cooch]

I just added a fairly long, somewhat technical section to Chapter 6 (new section 6.16), which goes through the steps of how to generate a 'model averaged' plot the relationship between a parameter and some environmental covariate of interest. The approach in Chapter 6 is based on 'first principles' (meaning, using the Delta method, and model averaging by hand). In the near future, I'll add some text to Chapter 11 on how you can accomplish much the same thing using the 'individual covariates' approach which Jeff references. At which point, Jeff will extend this thread, which currently only addresses plotting the estimates and CI for a 'single model' against some covariate.

[jlaake]

Actually the only practical difference in prediction with RMark between a single model and model averaging is that you specify a marklist of models to covariate.predictions rather than just a single model as the first argument. The function computes the set of real parameter estimates for each model and then model averages the set of real parameter estimates. Imagine a matrix with a row for each model and a column with the real parameter value for each set of covariates. It then computes a model average value for each column across rows (models). If the columns were a real parameter value for each occasion and the rows were for a Time (trend) model and a constant model. For the Time model each value would be different and for the constant model they would all be the same. These are then model averaged which would effectively reduce the slope and the amount of reduction would depend on the model weights.

regards--jeff

[cooch]

...In the near future, I'll add some text to Chapter 11 on how you can accomplish much the same thing using the 'individual covariates' approach ....

Done, and uploaded, as of 5 minutes ago...

[cooch]

The function computes the set of real parameter estimates for each model and then model averages the set of real parameter estimates.

Out of curiosity, how does RMARK handle the derivation of the 95% CI? In MARK, the CI is first generated on the transformed scale (say, logit),and then back-transformed to the real. The parameter estimates themselves are one thing, but the CI's? You could in theory do everything one either scale, but as I discovered, this does change the results slightly. For example, doing model averaging on the logit scale over set of models, and doing averaging on the back-transformed real scale, often yields slightly different answers (due to Jensen's inequality, as I remembered over the week-end.).

I suppose it doesn't much matter so long as you're consistent.

[jlaake]

Everything is done on the real scale for computation. Then back-transformed to set conf intervals and end points transformed back to real scale. I guess it could have all been done on link scale. Can't remember now why I chose that way.

--jeff

[cooch]

]

Everything is done on the real scale for computation. Then back-transformed to set conf intervals and end points transformed back to real scale. I guess it could have all been done on link scale. Can't remember now why I chose that way.

--jeff

Makes sense -- the issue arises because of the expression for calculating the unconditional variances for the model averaged parameter,



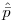it makes a difference (albeit, numerically small) on where/how you derive . If you do the averaging on the logit scale, then back-transform, you get a different average (and thus, different estimates of the unconditional variance) than if you back-transform the estimates for each model first, and then average -- and do subsequent calculations -- on the real scale. Jensen's inequality.

In other words, if you do



you'll get a different answer than if you do



and then Delta-back-transform this variance to the real scale.

As far as I can tell, the former approach is what MARK does in the individual covariate averaging routines (since this is what MARK does for 'normal' interval-specific model averaging, whereas I used the later approach for demonstrating the 'by hand' calculations in Chapter 6. The results are typically very close between the two approaches (difference often arising only in the 3rd decimal point and beyond), and I don't think there is a compelling theoretical reason to prefer one or the other (although perhaps there is a logical argument that could be made - distributional assumptions for the squared-term in the variance estimator, on logit versus real scale?)