Hi,
I am looking to evaluate heterogeneous survival in a model across groups and time.
Is it possible to develop a finite-mixture survival model (based on Pledger mixture Seber recoveries in RMark) that provides mixture proportions (pi) that are time and group dependent? Currently, I am aware of the capability to model mixed survival as group and time dependent but the output provides only a constant mixture proportion. Is there a straightforward path to estimating time-dependent proportions of the mixtures?
Secondly, what can I correctly interpret from the time and/or group dependent mixtures? In a two group mixture, can the proportions be a biologically interpretation of population structure?
Thanks for the help,
Drew
Time dependent mixture proportions in Seber finite-mixtures
9 posts
• Page 1 of 1
Re: Time dependent mixture proportions in Seber finite-mixtu
dfowler wrote:Hi,
I am looking to evaluate heterogeneous survival in a model across groups and time.
There are several different approaches to handling heterogeneity in MARK -- you mention the finite-mixture approach, but you might want to consider the logit-normal approach based on numerical integration of the individual RE. There is growing evidence that it is actually more robust than the finite mixture approach.
Is it possible to develop a finite-mixture survival model (based on Pledger mixture Seber recoveries in RMark) that provides mixture proportions (pi) that are time and group dependent? Currently, I am aware of the capability to model mixed survival as group and time dependent but the output provides only a constant mixture proportion. Is there a straightforward path to estimating time-dependent proportions of the mixtures?
Estimates of the mixture parameter,
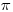 , are generally not interpretable. Using such mixture models gives you more robust estimation of other parameters, but the mixture parameter should not be interpreted, per se. Also, you can estimate a mixtures within groups, but not a temporally varying mixture parameter.
, are generally not interpretable. Using such mixture models gives you more robust estimation of other parameters, but the mixture parameter should not be interpreted, per se. Also, you can estimate a mixtures within groups, but not a temporally varying mixture parameter. Secondly, what can I correctly interpret from the time and/or group dependent mixtures? In a two group mixture, can the proportions be a biologically interpretation of population structure?
See above -- generally, nothing. Shirley Pledger (being the person who has done the most work with mixtures) strongly advises against it (in fact, this was one of the messages of her plenary at the most recent EURING meeting). See various sections in Chapter 14 of the MARK book, where mixture models are introduced.
- cooch
- Posts: 1665
- Joined: Thu May 15, 2003 4:11 pm
- Location: Cornell University
Re: Time dependent mixture proportions in Seber finite-mixtu
From an email I received from Shirley Pledger last year:
...the end being, mitigation of bias in estimates of model parameters in the presence of individual heterogeneity.
I have no belief in the intrinsic value or interpretability of the pi parameters or the other finite mixture parameters. I don't believe in the finite mixture groups as meaningful entities; they are just a means
to an end...
...the end being, mitigation of bias in estimates of model parameters in the presence of individual heterogeneity.
- cooch
- Posts: 1665
- Joined: Thu May 15, 2003 4:11 pm
- Location: Cornell University
Re: Time dependent mixture proportions in Seber finite-mixtu
And going back to Shirley's PhD and early papers she showed via simulation that the number of mixtures that might be 'selected' (using AIC or likelihood-ratio tests) doesn't necessarily correspond with the number of 'true' mixtures in the data. It's just a way to let p vary amongst individuals to try and get a more accurate estimate of N. The same holds for the use of finite mixtures in occupancy modelling.
And then there's the 'curse of Link' ...
Darryl
And then there's the 'curse of Link' ...
Darryl
- darryl
- Posts: 498
- Joined: Thu Jun 12, 2003 3:04 pm
- Location: Dunedin, New Zealand
Re: Time dependent mixture proportions in Seber finite-mixtu
darryl wrote:And going back to Shirley's PhD and early papers she showed via simulation that the number of mixtures that might be 'selected' (using AIC or likelihood-ratio tests) doesn't necessarily correspond with the number of 'true' mixtures in the data. It's just a way to let p vary amongst individuals to try and get a more accurate estimate of N. The same holds for the use of finite mixtures in occupancy modelling.
And then there's the 'curse of Link' ...
Darryl
Casting a long, discouraging shadow over all that is convenient and simple, he lurks...
- cooch
- Posts: 1665
- Joined: Thu May 15, 2003 4:11 pm
- Location: Cornell University
Re: Time dependent mixture proportions in Seber finite-mixtu
And of course, the curse of George Box: "All models are wrong, but ..."
- gwhite
- Posts: 340
- Joined: Fri May 16, 2003 9:05 am
Re: Time dependent mixture proportions in Seber finite-mixtu
gwhite wrote:And of course, the curse of George Box: "All models are wrong, but ..."
Indeed. And let's not forget:
The combination of some data and an aching desire for an answer does not ensure that a reasonable answer can be extracted from a given body of data. -- John Tukey
- cooch
- Posts: 1665
- Joined: Thu May 15, 2003 4:11 pm
- Location: Cornell University
Re: Time dependent mixture proportions in Seber finite-mixtu
Hi All,
Thanks for the comments regarding the interpretation of mixture proportions. These have been helpful. I'll also take a look into the logit-normal approach using individual random effects.
Drew
Thanks for the comments regarding the interpretation of mixture proportions. These have been helpful. I'll also take a look into the logit-normal approach using individual random effects.
Drew
- dfowler
- Posts: 2
- Joined: Tue Feb 13, 2018 1:47 pm
Re: Time dependent mixture proportions in Seber finite-mixtu
Are you trying to get estimates from mixtures to end up similar at some point in time,post-release, or have different banding cohorts have different mixtures?
- tlyons4
- Posts: 19
- Joined: Thu Nov 30, 2017 7:29 pm
9 posts
• Page 1 of 1
Who is online
Users browsing this forum: No registered users and 1 guest