www.phidot.org

by **cooch** » Tue Apr 24, 2012 3:40 pm

I've been working with Gary to add this to 'the book', but wanted to alert people about the general issue here (rather than the more passive approach of letting people stumble onto the new text as they read various chapters). Here is the text Gary sent me earlier today - if you're working with state-transition data types (MS models, robust design, Barker, occupancy...), you need to read this:

Various data types in MARK have state transitions. The multi-state data types are obvious, but the robust designs, Barker models, and the multi-season occupancy models all suffer from the same issue when the intervals between occasions are unequal.

To illustrate the issue, consider the case where an encounter occasion is missing in the multi-state data type. Consider the following valid MARK 5-occasion multi-state encounter history A.A00, where the missing occasion is shown as a dot and there are 2 states, A and B, and occasions are all 1 time unit apart. To explain this dot, several possibilities exist, namely:

$S_1^A\psi_1^{AA}(1-p_2^A)S_2^A\psi_1^AAp_3^{A}\dots~~~~\mbox{and}~~~~S_1^{A}\psi_1^{AB}(1-p_2^B)S_2^B\psi_2^{BA}p_3^A\dots$

However, suppose that you coded the data with the dot left out, and set the time intervals to 2, 1, and 1. That is, only 4 occasions are considered instead of 5. So the encounter history is now AA00. Unfortunately, this approach is going to give very different results from the proper parameterization above. MARK does not generate the probabilities for the transition to state B with this parameterization. The probability of surviving from occasion 1 to occasion 2 would now be $\left({S_1^{S}}\right)^2$ , with no consideration that the animal could have moved to state B during the missing occasion. So, even the survival estimates will be incorrect. The 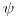$\psi$ parameters for the first interval are not comparable to the 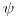$\psi$ parameters for the second and third intervals because they represent different time scales.

I have left the time interval correction on S, but have removed all time interval corrections from 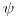$\psi$ . My logic is that when time intervals are “ragged”, e.g., 1.1, 0.9, 1.05, 0.95, it may still make sense to apply a correction to S. However, this correction is inappropriate for ψ, and may even be questionable for S. So, USER BEWARE!

The same general issue applies to the robust design data types and to the multi-season occupancy models. Consider the robust design with 3 primary occasions, each with 2 secondary occasions. Assume that the data were not collected for the 2nd primary, giving an encounter history of 11..11. The missing primary encounter history again can be explained by 2 possibilities:

$\dots S_1\gamma^{\prime\prime}_2S_2(1-\gamma_2^{\prime})\dots~~~~\mbox{and}~~~~S_1(1-\gamma_2^{\prime\prime})(1-p_2^{\ast})S_2(1-\gamma_3^{\prime\prime})\dots$

For the robust design data type, coding the encounter history as only 2 primary occasions, 1111, with time interval of 2 will give the correct parameterization for S (i.e. S^2

), but as above, the $\gamma^{\prime}$ and $\gamma^{\prime\prime}$ parameters cannot be corrected with this simple trick because the possibility of leaving the encounter area is not considered. So, for robust design data types (including the multi-state robust designs), only survival rates are corrected with the time interval, but none of the transition parameters are corrected. Again, USER BEWARE! Think carefully about what unequal time intervals may be doing to your interpretation of the parameter estimates.

Multi-season occupancy models also suffer the same issue, because extinction (ε ) and colonization (γ) can occur during a missing primary occasion. So, consider 3 primary occasions with 2 secondary occasions in each, with a missing 2nd primary: 11..11. Two possibilities again explain the missing primary:

$\dots\epsilon_2\gamma_2\dots~~~~\mbox{and}~~~~(1-\epsilon_2)(1p_^{\ast})(1-\epsilon_3)\dots$

So, simple power corrections to ε and γ are not appropriate, and MARK does not apply such a correction. The user will have to consider how unequal time intervals are affecting the interpretation of parameter estimates.

As shown in all the cases above, coding a missing primary occasion with a set of dots should provide the necessary correction, although issues of parameter estimability come up. That is, unique estimates of the time-varying transition and survival probabilities are not possible, so the user will have to set some constraints to make the parameters estimable.

by **Eurycea** » Fri Jun 08, 2012 6:46 pm

Thanks for posting this. I had no idea about this, and I have a lot of unequal intervals in our RD data and nothing I can do about it from a sampling standpoint. Any hints on how to interpret the estimates with unequal time intervals?

edited to add: I guess I'm thinking, for example, about (.) models or any models that call for equal estimates across time intervals with the gamma parameters in a RD. I take this to mean that if you're testing a (.) model with unequal time intervals, say random emigration, you're not ACTUALLY testing the hypothesis that random emigration is equal across time intervals, since the unequal intervals in the data mean the actual estimates of gamma will be different. Say gamma is 0.5 across years, and you want to test that it is equal, but your sample intervals are spaced such that there are missing years, or large gaps between years, then testing a (.) model would not give you a gamma of 0.5. Does this make sense? I suppose I can play with simulated data and see what happens...

by **claudiapenaloza** » Tue Jan 28, 2014 9:37 pm

I want to add an aside here...

When including dots "." for those missing primary periods in, for example, a Robust Design, you need to add a minimum of TWO DOTS PER PRIMARY PERIOD, that is, two secondary sessions per primary period, even though it was not sampled.

Hope this is useful!

cheers,
claudia

by **Jochen** » Wed Feb 26, 2014 12:37 pm

I wonder if the same is true for the pent and d estimates in occupancy models with relaxed closure assumption, as recently added to MARK. I guess entry and departure are somewhat similar to extinction and colonization in RD, but I would like to be sure before creating huge inp files with all the missing occasions.

Thanks for suggestions
Jochen

www.phidot.org

unequal intervals & state-transition models

unequal intervals & state-transition models

Re: unequal intervals & state-transition models

Re: unequal intervals & state-transition models

Re: unequal intervals & state-transition models

Who is online